Kreis - Kreisfläche

Wir schauen durch zwei runde Augen auf eine Welt voller Kurven und Kreise, so sehen wir zum Beispiel die Sonne und den Mond kreisrund am Himmel stehen. Züge, Autos oder Fahrräder rollen auf runden Rädern zu ihren Zielen und wir besiegeln mit runden Ringen eine Verlobung oder Ehe. Ein Kreis ist ein perfektes Gebilde ohne Anfang und Ende.

Die Geometrie des Kreises

In der Geometrie definiert sich ein Kreis als Menge aller Punkte auf einer Ebene, die den gleichen Abstand zu seinem Mittelpunkt(M) haben. Dieser Abstand zwischen dem Mittelpunkt und den Kreispunkten nennt sich Radius(r). Er ist immer eine positive reelle Zahl. Der Durchmesser(d) ist die Stecke zwischen zwei gegenüberliegenden Kreispunkten, die durch den Mittelpunkt führt. Er hat die doppelte Größe des Radius des Kreises.

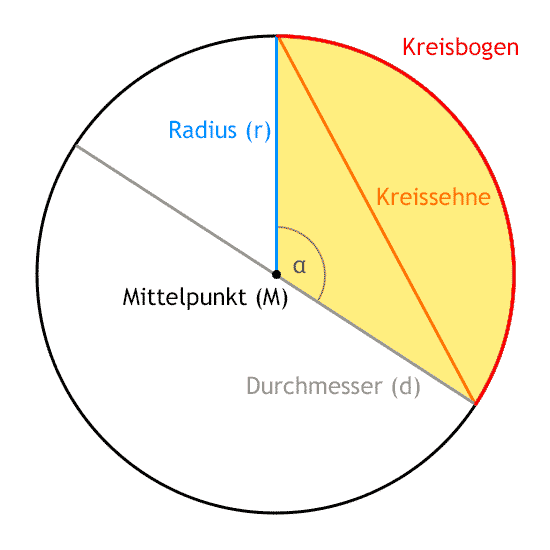
Der Kreis zählt zu den klassischen und grundlegenden Objekten der Geometrie, schon in der griechischen Antike stieß der Kreis, Aufgrund seiner Vollkommenheit auf großes Interesse. Ein Kreis ist eine eindimensione Kurve, er steht also nur aus den Kreispunkten. Die Fläche die von den Kreispunkten umschlossen wird ist die Kreisfläche oder auch Kreisscheibe.

Eine zusammenhängende Teilmenge der Kreislinie bezeichnet man als Kreisbogen, die Strecke, die die beiden Endpunkte des Kreisbogens verbindet, nennt man Kreissehne, zu jeder Sehne gehören zwei Kreisbögen, die zusammen den Kreis ergeben. Die längste Kreissehne ist der Durchmesser, hier verläuft die Kreissehne durch den Mittelpunkt und die beiden Kreisbögen heißen Halbkreise.

Ein Kreisausschnitt (Kreissektor) ist die Fläche die von zwei Radien und dem Kreisbogen zwischen den beiden Radien umschlossen wird.

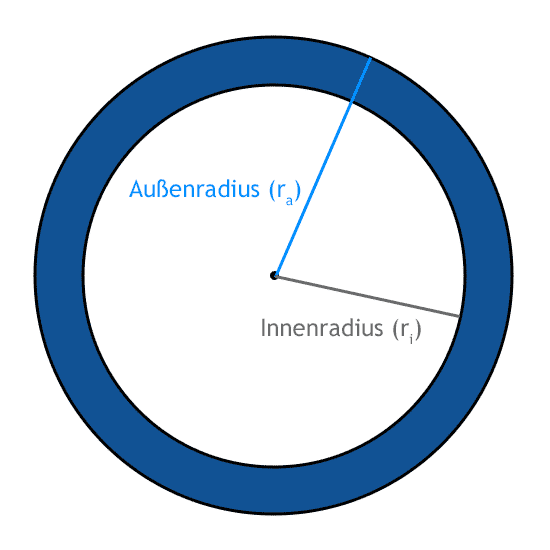
Ein Kreisring erhält man, wenn man aus einer Kreisfläche eine kleinere Kresifläche mit demselben Mittelpunkt herausschneidet.

Für die Lage einer Gerade in Bezug auf einen Kreis gibt es 3 Varianten.

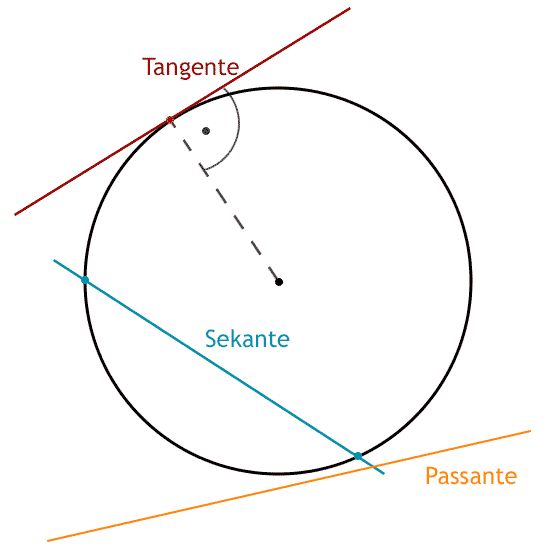
Die Sekante schneidet den Kreis in zwei Teile. Gerade und Kreis haben zwei Schnittpunkte. Läuft die Gerade auch noch durch den Mittelpunkt kann man die Sekande auch als Zentrale bezeichnen.

Die Tangente gerührt und tangiert den Kreis an einem einzigen Punkt. Der Abstand zwischen Mitelpunkt des Kreises und des Punktes andem die tangente den Kreis berüht ist genau so groß wie der Radius den Kreises. Die Tanget steht an diesem Punkt senkrecht zum Radius.

Die Passante passiert den Kreis ohne ihn zu berühren oder zu schneiden.