Sechseck - Hexagon

Die Bienen tun es, die Moleküle und die Kristalle tun es auch - sie bilden Sechsecke oder sechseckige Formen. Die Geometrie der Waben ist die effizienteste und stabilste Form, die in der Natur vorkommt.

Bei den sechseckigen Reihen wird das höchstmögliche Fassungsvermögen und das Maximum an umbauten Raum mit geringsten Materialaufwand umbaut, und dies gleichzeitig bei größter Stabilität. Die perfekte Struktur der Zellen in den Bienenwaben ließ Johannes Kepler vermuten, Bienen hätten einen mathematischen Verstand. Warum und wie die Bienen nun genau ihre Waben aus solch perfekten Sechsecken bauen, ist bis heute noch nicht restlos geklärt.

Die Geometrie den Sechsecks

Ein Sechseck, auch Hexagon genannt, ist ein Vieleck (Polygon), das aus sechs Ecken und sechs Seiten besteht.

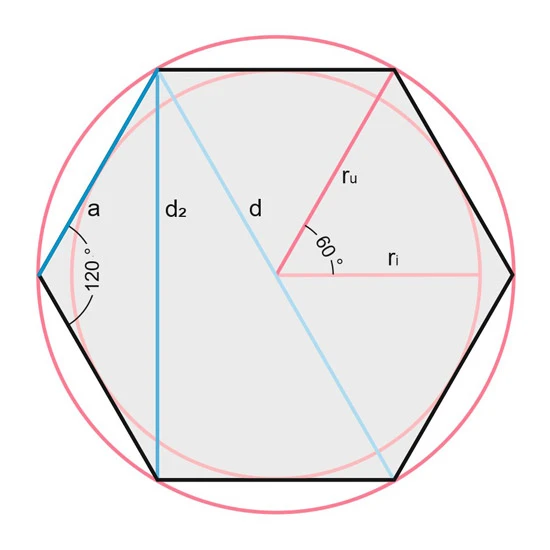
Sind alle sechs Seiten gleich lang, sind auch die sechs Innenwinkel gleich groß und betragen 120 °. In diesem Fall spricht man von einem gleichseitigen oder regulären Sechseck.

Ein reguläres Sechseck läßt sich auch aus sechs gleichgroßen, gleichseitigen Dreiecken zusammensetzen.

Konstruktion von Sechsecken

Konstruktion mit einem Zirkel

Können Sie sich noch an Ihre Schulzeit erinnern, als der Umgang mit dem Zirkel gelehrt wurde? Eine meiner liebsten Übungen war die Zirkelblume.

Man zieht einen Kreis mit dem Zirkel und behält den Radius eingestellt. Dann sticht man mit dem Zirkel auf den eben gezeichnete Kreis ein und zeichnet einen Kreisausschnitt vom Kreis über den Mittelpunkt wieder zum Kreis. Dann sticht man an einem der Schnittpunkte den Kreises mit dem Kreisausschnitt ein und wiederholt den Vorgang solange bis man dem Kreis herum ist und man eine 6 blättrige, symmetrische Blüte erhalten hat.

Wenn man dann die Schnittpunkte am Kreis nacheinander mit einem Linieal verbindet, erhält man ein gleichseitiges Sechseck.

 

Konstruktion nach Euklid

Der griechische Mathematiker Euklid schlägt eine etwas andere Vorgehensweise vor.

Man zieht zuerst eine Gerade, auf dieser legt man den Mittelpunkt des dann zu zeichnenden Kreises fest und behält den Radius im Zirkel. An einem der Schnittpunkte der Geraden mit dem Kreis sticht man mit den Zirkel ein und zieht einen Kreisausschnitt vom Kreis über dem Mittelpunkt wieder zum Kreis. Dann zieht man zwei Geraden je von einem Schnittpunkt des Kreisausschnittes mit dem Kreis durch den Mittelpunkt zur gegenüberliegenden Seite des Kreises.

Auch hier erhält man ein reguläres Sechseck, wenn man dann die Schnittpunkte am Kreis nacheinander mit einem Linieal verbindet.

 

Konstruktion aus einer gegebenen Seitelänge a

Man kann ein Sechseck auch konstruieren, wenn man nur eine gegebenen Seitenlänge hat.

Hierzu nimmt man die Seitenlänge als Radius in den Zirkel und zieht von jedem Ende der Seite einen Kreisbogen bis sich beide Kreisbögen schneiden - dies ist dann der Mittelpunkt. Den Radius behält man im Zirkel und zeichnet einen Kreis um den eben konstruierten Mittelpunkt. Der Kreis berüht die beiden Enden der Strecke mit der bekannten Seitenlänge.

Dieser Kreis ist der Umkreis des zu zeichnenden Sechsecks. Jetzt trägt man, beginnend von einem Ende mit dem Zirkel nacheinander die Strecke den Radius entlang des Umkreises ab. Diese Punkte sind dann die Eckpunkte des Hexagons.