Bilder-plus.de
☰ zu

Die Bildergleichung – Größenberechung einer Projektionsleinwand

Warum die Mathematik auch im Atelier gebraucht wird?

Wer kann sich noch an die Sachaufgaben in Mathematik erinnern? An Gleichungen mit 2 Unbekannten? Und die Frage, wann brauche ich dies denn jemals außerhalb der Schule? Als Ingenieur, Programmierer oder Physiker vielleicht, aber als Bildermacher?

Heute früh bekam ich noch vor dem ersten Kaffee folgenden Anfrage: "Guten Morgen Herr Ertel, ein Kunde wünscht eine schallabsorbierede Projektionsleinwand mit einer Diagonalen von 2,5 Meter und dem Format 16/9..."

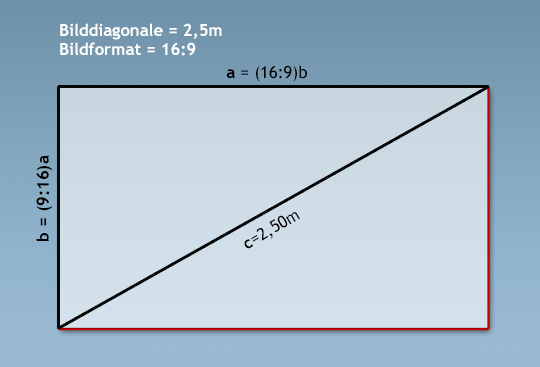
Projektionsfläche mit einer Diagonalen von 2,5m

Und da ist sie, die mathematische Sachaufgabe.
Zuerst fiel mir natürlich der Satz des Pythagoras ein a²+b²=c², mit der Vorgabe c=2,5m und bei einem Bildformat von 16/9 ist a=(16:9)b und b=(9:16)a

Um die Gleichung mit den zwei Unbekannten Bildbreite und Bildhöhe zu lösen, haben wir diese beiden Gleichungen zur Verfügung a² + b² = (2,5)² = 6,25
b = (9:16)a = 0,5625a
Zu einer Gleichung zusammenfassen a² + (0,5625a)² = 6,25
Auflösen nach Potenzgesetzen

a² + 0,5625² x a² = 6,25
Ausrechnungen 0,5625² a² + 0,3164a² = 6,25
Addieren von 1a² + 0,3164a² 1,3164a² = 6,25
Beide Seiten durch 1,3164 teilen a² = 4,7478
Auf beiden Seiten die Quadratwurzel ziehen

a = 2,1789
Aus dem Seitenverhältniss von 16/9... b = (9:16)a = 0,5625 x 2,1789
...kann man nun die Bildhöhe berechnen b = 1,2256

Mit diesem Ergebnis kann ich nun den Preis für die schallabsorbierende Projektionsfläche in der Größe von 2179 mm x 1226 mm berechnen.

 

Weitere Links

 

Zum Seitenanfang