Kreis – Kreisfläche
Wir schauen durch zwei runde Augen auf eine Welt voller Kurven und Kreise: Sonne und Mond erscheinen kreisrund, Räder rollen auf runden Bahnen, Ringe stehen für Verbundenheit. Ein Kreis ist ein perfektes Gebilde ohne Anfang und Ende. In diesem Artikel geht es um die Geometrie des Kreises – und um die wichtigsten Formeln für Radius, Durchmesser, Umfang und Kreisfläche.
Die Geometrie des Kreises
In der Geometrie definiert sich ein Kreis als Menge aller Punkte auf einer Ebene, die den gleichen Abstand zu seinem Mittelpunkt (M) haben. Dieser Abstand zwischen Mittelpunkt und Kreislinie heißt Radius (r) und ist immer eine positive reelle Zahl.
Der Durchmesser (d) ist die Strecke zwischen zwei gegenüberliegenden Punkten auf der Kreislinie, die durch den Mittelpunkt führt. Er hat die doppelte Größe des Radius: d = 2r.
Der Kreis zählt zu den klassischen und grundlegenden Objekten der Geometrie. Schon in der griechischen Antike stieß der Kreis aufgrund seiner Vollkommenheit auf großes Interesse. Ein Kreis ist eine eindimensionale Kurve, er besteht also aus der Kreislinie. Die Fläche, die von dieser Linie umschlossen wird, bezeichnet man als Kreisfläche oder Kreisscheibe.
Kreisfläche schnell berechnen
Mit dem Kreisflächen-Rechner hier auf der Seite lassen sich bequem aus einem Wert für Radius, Durchmesser, Umfang oder Kreisfläche alle anderen Werte bestimmen:
- Zuerst einen Eingabemodus wählen und den vorhanden Wert eingeben.
Das Modul berechnet Radius, Durchmesser, Umfang und Kreisfläche.
Kreisflächen-Rechner
Eingabe: – cm · Modus: –
Kreisbogen, Sehne, Sektor und Ring
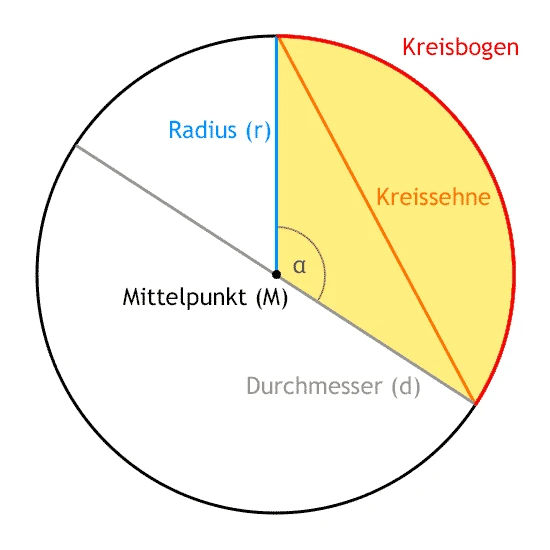
Eine zusammenhängende Teilmenge der Kreislinie bezeichnet man als Kreisbogen. Die Strecke, die die beiden Endpunkte eines Kreisbogens verbindet, nennt man Kreissehne. Zu jeder Sehne gehören zwei Kreisbögen, die zusammen den Kreis ergeben. Die längste Kreissehne ist der Durchmesser – er teilt den Kreis in zwei Halbkreise.
Formeln zu Kreisbogen, Sehne, Sektor und Ring (Überblick)
- Länge Kreisbogen: LB = r · α
- Länge Kreissehne: LKS = 2 · r · sin(α/2)
- Fläche Kreissektor: ASK = (r²/2) · α
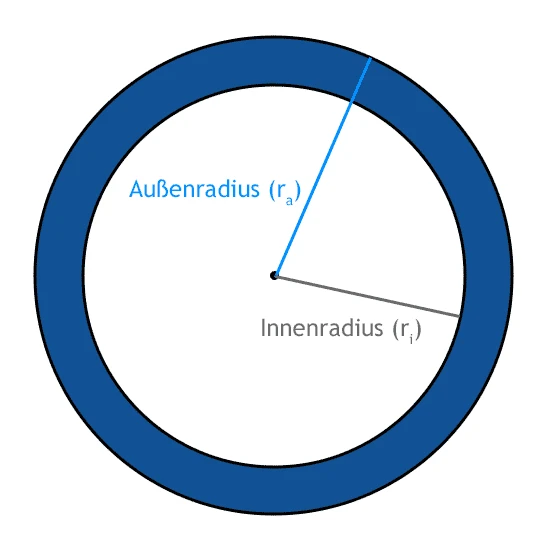
- Fläche Kreisring: KR = π · (ra² − ri²)
Ein Kreisausschnitt (Kreissektor) ist die Fläche, die von zwei Radien und dem dazwischenliegenden Kreisbogen umschlossen wird.
Ein Kreisring entsteht, wenn man aus einer Kreisfläche eine kleinere Kreisfläche mit demselben Mittelpunkt herausschneidet.
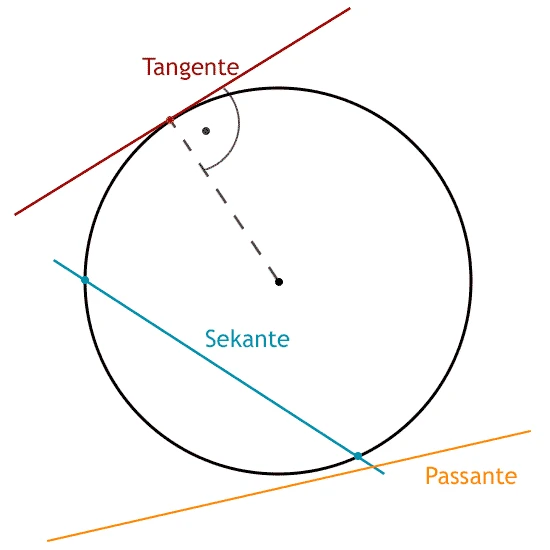
Sekante, Tangente und Passante
Für die Lage einer Geraden in Bezug auf einen Kreis gibt es drei typische Varianten:
Sekante: Die Gerade schneidet den Kreis in zwei Punkten. Verläuft sie zusätzlich durch den Mittelpunkt, spricht man auch von einer „Zentrale“.
Tangente: Die Gerade berührt den Kreis in genau einem Punkt. Der Radius steht im Berührpunkt senkrecht auf der Tangente.
Passante: Die Gerade verläuft am Kreis vorbei, ohne ihn zu schneiden oder zu berühren.