Praxisbeispiel: Die Bildergleichung
Größenberechnung einer Projektionsleinwand im Format 16:9
Ein Kunde wünscht eine schallabsorbierende Projektionsleinwand mit 2,5 m Diagonale im Format 16:9 – und plötzlich ist sie da: die klassische Sachaufgabe mit zwei Unbekannten. Mit Seitenverhältnis und Satz des Pythagoras lassen sich Bildbreite und Bildhöhe eindeutig bestimmen.
Wozu Mathematik im Atelier gebraucht wird
Wer kann sich noch an die Sachaufgaben in Mathematik erinnern? An Gleichungen mit zwei Unbekannten – und an die Frage: „Wann brauche ich das jemals außerhalb der Schule?“ Als Ingenieur, Programmierer oder Physiker vielleicht. Aber als Bildermacher?
Heute früh bekam ich noch vor dem ersten Kaffee folgende Anfrage: „Guten Morgen Herr Ertel, ein Kunde wünscht eine schallabsorbierende Projektionsleinwand mit einer Diagonalen von 2,5 m und dem Format 16/9…“
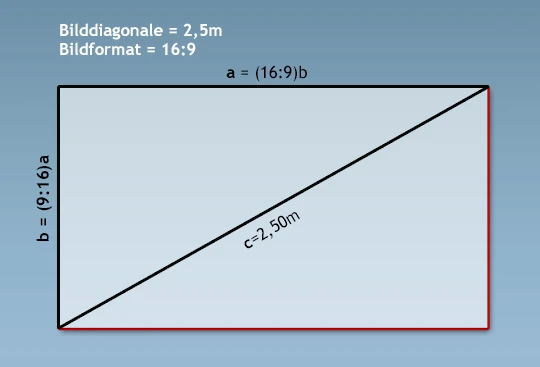
Und da ist sie – die mathematische Sachaufgabe. Wir kennen:
- Diagonale: c = 2,5 m
- Format: 16:9 (Breite: Höhe)
- Pythagoras: a² + b² = c²
- Seitenverhältnis: b = (9/16) · a
Schritt für Schritt zur Breite und Höhe
| Schritt | Rechnung |
|---|---|
| 1) Pythagoras mit c | a² + b² = (2,5)² = 6,25 |
| 2) Seitenverhältnis einsetzen | b = (9/16) · a = 0,5625 · a |
| 3) Zusammenfassen | a² + (0,5625a)² = 6,25 |
| 4) Auflösen | a² + 0,31640625a² = 6,25 → 1,31640625a² = 6,25 |
| 5) Nach a² | a² = 6,25 / 1,31640625 ≈ 4,7478 |
| 6) Wurzel ziehen | a ≈ 2,1789 m |
| 7) Höhe berechnen | b = 0,5625 · 2,1789 ≈ 1,2256 m |
„Diese Kombination aus Seitenverhältnis und Pythagoras nenne ich gern die Bildergleichung – weil sie im Atelier genauso oft gebraucht wird wie im Mathematikunterricht.“ K.D.Ronny Ertel
Ergebnis in Praxismaßen
Damit ergibt sich für die Projektionsfläche:
- Breite: a ≈ 2,1789 m → 2179 mm
- Höhe: b ≈ 1,2256 m → 1226 mm
Mit diesem Ergebnis kann ich nun den Preis für die schallabsorbierende Projektionsfläche in der Größe 2179 mm × 1226 mm berechnen.
